04Bootstrap

Bootstrap(自助法取样)

Bootstrap 的思想是生成一系列 bootstrap 伪样本，每个样本是初始数据有放回抽样。通过对伪样本的计算，获得统计量的分布；当样本数量非常大时，每次抽样中不是重复的样本概率趋近为 0.632，故该抽样方法也叫 0.632 自助法

置信区间估计

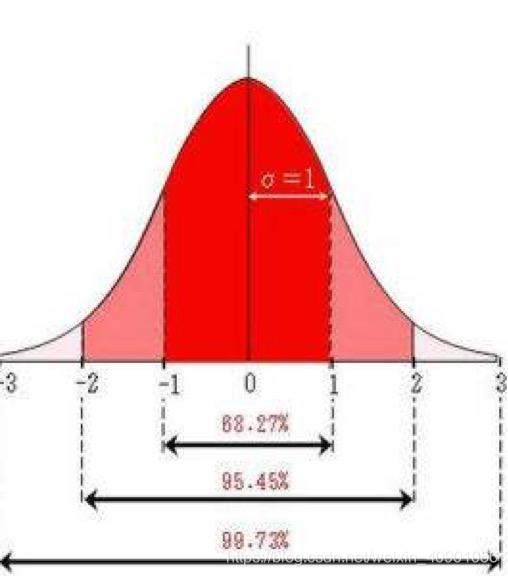
在正态分布情况下对统计量的置信区间进行估计，在标准正态分布中最常用的就是95%置信区间；从公式上演化推断均值的95%置信区间就是：

$$\begin{equation}
\mu-1.96\sigma \le X\le\mu+1.96\sigma
\end{equation}$$

但事实上，当找不到合适的分布时，就无法用标准的正态分布计算置信区间了。但幸运的是有一种随机化的方法可以用于计算
非参数分布的置信区间。通过对小样本数据的有放回抽样近似的估计总体的分布，例如我们对包含30个小样本的测试数据进行平均值置信区间估计。

实现步骤

+ 随机进行1000次有放回的抽样，每次抽样从数据集中抽取30个样本
+ 每次抽样后计算当前抽样状态的平均值
+ 最后得到1000次抽样的平均值分布
+ 使用百分位数方法估计平均数的置信区间

代码实现

np.random.seed(100)
testData=np.random.normal(loc=0.0, scale=1.0,size=30)
testData=pd.DataFrame(testData.reshape(-1,1))
print(f"mean of random sample: {testData[0].mean()}")
def bootstrap(inputData,sampleTimes=1000):
    timesCount=inputData.shape[1]
    meanArray=np.empty((0,timesCount))
    for item in range(0,sampleTimes):
        item_mean=inputData.apply(sample_mean_items,axis=0)
        meanArray=np.vstack([meanArray,item_mean])
    #! 95% confidence interval
    #* 2.5 Quantile and 97.5 Quantile
    confidenceInterVal=[]
    #? 0 base
    for timepint in range(0,timesCount):
        meanData=np.mean(meanArray[:,timepint])
        lowData=np.percentile(meanArray[:,timepint],97.5)
        highData=np.percentile(meanArray[:,timepint],2.5)
        confidenceInterVal.append((lowData,meanData,highData))
    return confidenceInterVal      
print(f"Bootstrap InterVal:{bootstrap(testData)[0]}")

#mean of random sample: 0.16454200588058832
#Bootstrap InterVal:(0.4530127407922769, 0.16330846106758692, -0.10604181823280227)

当进行1000次抽样后,将每次抽样得到的均值存入meanArray数组，再调用np.percentile计算均值的置信区间

参考

1. https://www.knowledgedict.com/tutorial/ml-bootstrap-sample.html
2. https://www.jianshu.com/p/275d7618d9a5