PCA降维打击

1.PCA的基本原理

主成分分析（Principle component analysis）简称PCA，是常用的降维方法之一。通过将n维的数据集降维到n’低纬度空间；使得降维之后数据集尽可能的代表原数据集同时降维之后的损失尽可能的小。

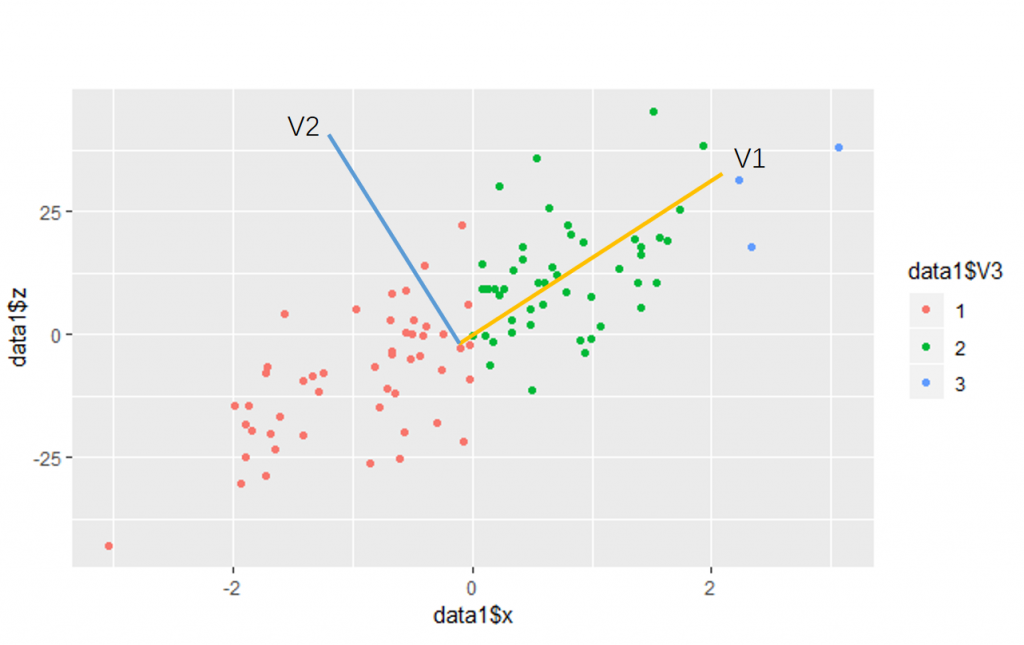
如图1所示，在R中使用rnorm函数生成正态分布数据集在二维空间的分布；我们希望找到一个维度能够代表数据集在二维空间中的分布特征，而这样的维度有无数种.如何找到最好的那个维度使得数据集经过变换后尽可能的保留原始数据集的特征。

​ 图1中有V1与V2两个一维的特征向量，从图1中可以看出在V1特征向量上能够更好的反应原始数据集的特征。数据集映射在V1的方向上进行映射后，映射后的数据集从低纬度重构出高纬度数据集D’，使得D’与原始数据集尽可能的相似，也就是D’中的点与原始数据集中的点的距离最小；或者可以从另一个角度理解为原始数据经过映射后在低纬空间中可以区分开来。这对应着PCA中两种优化目标：最近重构性与最大可分性。同样的当数据集从二维推广到任意维度时，我们的优化目标也就变成样本点在一个超平面进行重构后的距离最近或者在映射到超平面后样本内方差最大化。

2.1基于最近重构性进行优化

假定我们有一个m个n维的数据集 ，假定在每个维度上都进行了中心化，并且将原先的n维属性投影到新的坐标系使得这n个维度的属性构成标准的正交基向量 )，即任意两个w满足 ；进行正交化主要是考虑在降维的过程中，任意两个主成分之间应该尽可能的保留更多的信息，不存在相关性。

假设将数据从n维降到k维（k<n）,则第样本点 在k维的投影坐标 其中 表示样本i在降维后第j个维度上的投影坐标。通过投影坐标 与标准正交基向量 )重构出原始数据 。

优化目标是使得所有重构出的样本与原始样本的累积距离最小。

具体的公式推导可以看这个博主写的

2.2基于最大可分性进行优化

​ 从最大可分性角度出发，优化目标是使得样本点在降维后的平面的投影尽可能的分开，相当于投影后的样本方差最大。

3.算法流程

​ 假定数据集包含m个n维数据。

• 将原始数据按照n行m列进行排列
• 在每一个维度上进行中心化，也就是每个数据减去同一行中的均值方便后面的计算
• 计算数据集的协方差矩阵
• 对协方差求取特征值与特征向量
• 将特征向量 按照其特征值大小从上至下排列成矩阵
• 根据认为设定的K值，将数据集映射到K维的低纬空间

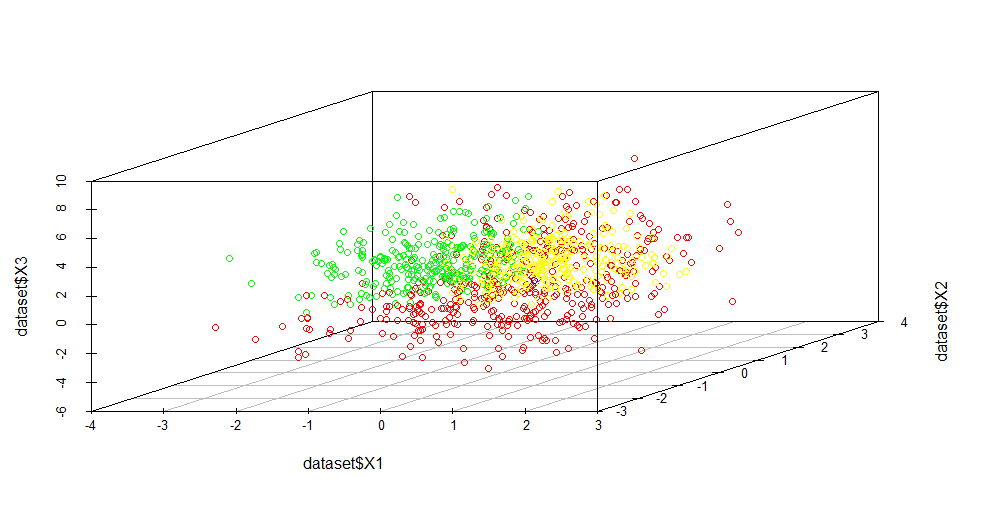
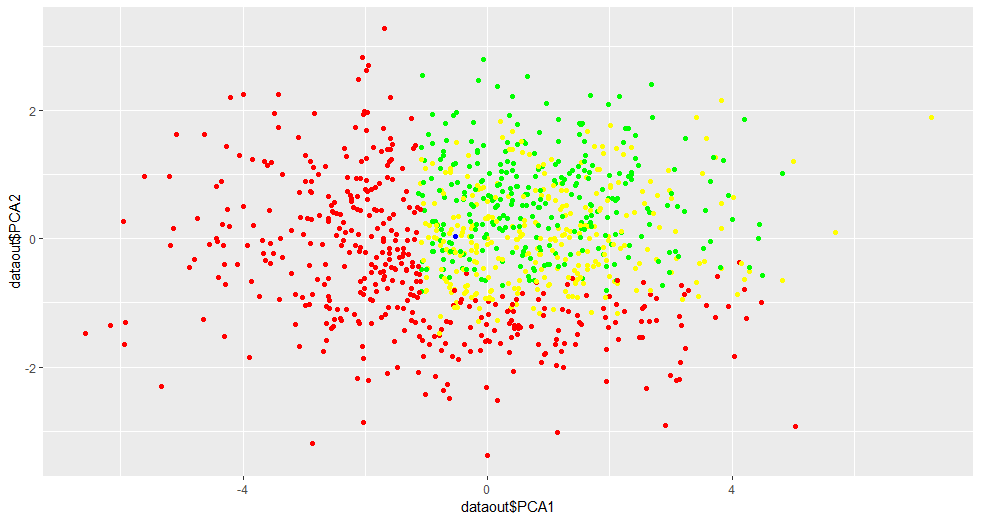
4.1实例

​ 随机生成1000个3维数据集，并对其中的点打上标签如图2所示。当保留样本中65%的变异时，才使得数据集从3维降低到2维，如图3所示；而此时黄色和绿色样本之间仍旧没有完全区分开来可能是由于它们之间的区分确实不明显。同样从图3中也可以发现一些样本偏离比较远，在某种程度上可以认为是人为因素产生的噪声数据

4.2图片数据降维

使用UCI中的Yale数据集，数据集中包括了21个志愿者在四种心情状态，4种角度以及是否戴眼镜的图片数据。从中随机选取了10位志愿者，在某一种状态下进行图片数据的降维处理。从图4可以看出当保留原始数据90%的差异时，图片与原图的差异不是很大，但仍旧有一些图片还是与原始数据相比丢失的比较多；随着保留差异程度逐渐减少，重构数据相比原始数据丢失的越来越多，在图片上表现也就越来越不清晰。

对带上眼镜的图片数据进行同样的处理，如图4所示当保留90%的差异进行重构时，仍旧可以看出大概。通过PCA的简单降维，可以在保证图片质量的情况下牺牲图片的清晰度；一定程度上节省了带宽。

5总结

• PCA计算方法简单，运用了矩阵特征值分解
• 计算过程中使用协方差矩阵，保证了各个维度之间不会有相互影响，使得特征值分解时数据存在重叠的情况
• PCA降维后的特征值在解释程度上不如原始样本
• 舍弃的一些方差信息，有时候可能是区分一些特定样本的重要信息
• 使用核化的方法对复杂数据进行PCA

6数据集与代码

6.1图片加载函数

# coding=utf-8
import os
import numpy as np
from PIL import Image

'''
单张图片的读取与图片向矩阵数据的转换
    #p2与p4可以正常读取
    img = Image.open("D:\\pycharm\\project\\pca\\faces\\an2i\\an2i_left_angry_open_2.pgm")
    #颜色变成黑白，本来就是黑白的就省去这一步就行了
    img2=img.convert("L")
    img2.show()
    data=img.getdata()
    data=np.matrix(data)
    print(data)
'''
def loadpgm(filepath):
    first_file=True
    for root, dirs, files in os.walk(filepath):
        #人名
        rootpicture=root.split("\\")[-1]+".jpeg"
        for file in files:
            #print(os.path.splitext(file)[0][-1])
            #文件后缀名
            if first_file:
                if os.path.splitext(file)[0][-23::] == "left_angry_sunglasses_2":
                    img = Image.open((os.path.join(root, file)))
                    oneperson = img.getdata()
                    img.save(rootpicture)
                    oneperson = np.array(oneperson).tolist()
                    first_file=False
            else:
                if os.path.splitext(file)[0][-23::] == "left_angry_sunglasses_2":
                    img = Image.open((os.path.join(root, file)))
                    rootimg = Image.fromarray(np.array(img.getdata())).convert("RGB")
                    rootimg.save(rootpicture)
                    oneperson=oneperson+(np.array(img.getdata()).tolist())
                #img.show()
                #print(img.size)
    return np.array(oneperson)

6.2文件读取函数

def readfile(path):
    file = open(path)
    next(file)
    first_else = True
    for data in file.readlines():
        data = data.strip("\n")
        nums = data.split("\t")[0:3]
        if first_else:
            matrix = np.array(nums)
            first_else = False
        else:
            matrix = np.c_[matrix, nums]
    file.close()
    # 矩阵为n*m，m为样本数
    return np.mat(matrix).astype(float)

6.3数据中心化

def zeroScale(dataset):
    # 对数据集按行求平均
    meanVals = np.mean(dataset, axis=1)
    # 中心化
    zerodata = dataset - meanVals
    return zerodata

6.4特征值范围

def eigvalPc(eigVals, precentages):
    # 特征值从大到小排序
    sortArray = np.sort(eigVals)[::-1]
    # 百分比
    arrSum = sum(sortArray)
    tmpSum = 0
    num = 0
    for i in sortArray:
        tmpSum += i
        num += 1
        if tmpSum/arrSum >= precentages:
            ##返回最后的特征值下标
            return num

6.5PCA函数

def pca(dataset, precentages):
    meanVals = np.mean(dataset, axis=1)
    # 中心化
    zerodata = zeroScale(dataset)
    # 计算协方差矩阵
    covMat = np.cov(zerodata)
    eigVals, eigVects = np.linalg.eig(np.mat(covMat))
    k = eigvalPc(eigVals, precentages)
    # 获取对应的特征值排好序的下标
    eigIndex = np.argsort(eigVals)[::-1]
    # 获取对应的特征向量下标
    eigIndex = eigIndex[0:k + 1]
    # 获取主成分特征向量
    eigPCA = eigVects[:, eigIndex]
    # 原始数据投影到低纬数据
    lowDimdata = np.transpose(zerodata) * eigPCA
    #重构数据
    reconMat=(lowDimdata*np.transpose(eigPCA))+np.transpose(meanVals)
    #np.savetxt(outfile, reconMat, delimiter="\t")
    return  reconMat

6.5图片生成与保存

# coding=utf-8
import os
import numpy as np
from loadpgm import loadpgm
from PIL import Image
if __name__ == "__main__":
    for root, dirs, files in os.walk("D:\\pycharm\\project\\pca\\faces\\"):
        first_person = True
        for dir in dirs:
            filepath = (os.path.join(root, dir))
            if first_person:
                dataset = loadpgm(filepath)
                first_person = False
            else:
                dataset = np.column_stack((dataset, loadpgm(filepath)))
    #数据矩阵化
    dataset=np.mat(dataset)
    out=pca(dataset,0.7)
    #10张图片10*3840每张图片为60X64
    for i in range(0,10):
        outpicture=str(i)+".jpeg"
        picture1 = (out[i].reshape(60, 64))
        # 保存重构图片数据
        picture1 = np.real(picture1)
        picture1 = Image.fromarray(picture1).convert("RGB")
        picture1.save(outpicture)

图片数据与PCA源代码上传到我的github仓库中

参考

1.机器学习[周志华版]

2.PCA定义：http://blog.codinglabs.org/articles/pca-tutorial.html

3.公式推导：http://www.cnblogs.com/pinard/p/6239403.html

4.主要代码：http://www.cnblogs.com/chenbjin/p/4200790.html

5.pgm数据处理：https://blog.csdn.net/xijuezhu8128/article/details/79661016

6.numpy包处理：https://blog.csdn.net/qq_43287650/article/details/83211898